Understanding the Gaussian output file

For easier analysis, let’s drag all of our files back onto our personal laptop using FileZilla. (If you want you can try to read the Gaussian .log file in the terminal, but you’ll soon see why that’s not going to scale well.)

We won’t use the fort.7 file and eqMeCyhex_oe has a total size of 0 bytes (i.e., there’s nothing written in it) so for the sake of cleanliness we can delete those. First, let’s look at our optimized structure to make sure the final geometry makes chemical sense. Open eqMeCyhex.log in GaussView (download it from the code repo if you’re not following along).

If you're using GaussView5 with Gaussian16 you'll most likely run into this error: Don't panic, this issue occurs because g16 writes some extra information in the output file that GaussView5 doesn't know how to handle. Use this script provided by Dr. Davor Šakić from the University of Zagreb to generate a output file that GaussView5 can read.

GaussView shows us a perfectly normal equatorial methylcyclohexane.

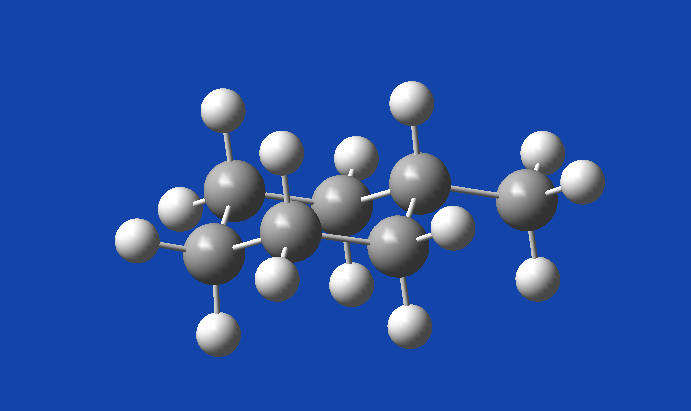
You should always check your structures to make sure they are generally expected since not all mathematical solutions are physical ones. Sometimes our jobs will give us chemically nonsensical solutions simply because the algorithm found a particular energy well that it couldn’t get out of.

The computers are here to do your math, not your thinking.

Fantastic, let’s grab some numbers. One of the first things we noticed is that eqMeCyhex.log is just a really long text file that GaussView5 is able to generate a picture from. So, open eqMeCyhex.log in a text editor (or follow along in another window using the link above) and we search the output for energies and vibrational/thermochemical data.

First we’ll want to check for imaginary (negative) vibrational frequencies which indicate saddle point structures. Search eqMeCyhex.log for Harmonic frequencies:

...
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
 activities (A**4/AMU), depolarization ratios for plane and unpolarized
 incident light, reduced masses (AMU), force constants (mDyne/A),
 and normal coordinates:
                      1                      2                      3
                      A                      A                      A
 Frequencies --    159.1459               229.6806               248.3997
 Red. masses --      2.2917                 1.2669                 1.3457
 Frc consts  --      0.0342                 0.0394                 0.0489
 IR Inten    --      0.0025                 0.0069                 0.0006
...

Gaussian prints all vibrational frequencies in the output in ascending order so we only need to check the first entry to ensure that all our vibrational frequencies are real.

Next, we’ll calculate the energy for our optimized structure. At this point, I highly recommend that you read this technical document from Dr. Joseph Ochterski about thermochemistry in Gaussian.¹ It describes how Gaussian calculates various thermochemical values and their proper usage in computing ΔG_rxn. Searching eqMeCyhex.log for correction produces:

...
 Zero-point correction=                           0.198783 (Hartree/Particle)
 Thermal correction to Energy=                    0.204789
 Thermal correction to Enthalpy=                  0.205654
 Thermal correction to Gibbs Free Energy=         0.171472
 Sum of electronic and zero-point Energies=           -274.642438
 Sum of electronic and thermal Energies=              -274.636431
 Sum of electronic and thermal Enthalpies=            -274.635566
 Sum of electronic and thermal Free Energies=         -274.669748
...

With most ab initio methods absolute energies of molecular systems are calculated relative to free electrons and nuclei which is why they are large and negative.

By default, Gaussian reports energies in Hartree atomic units ($E_h$ or A.U.):

The values we’re interested in are:

 Thermal correction to Gibbs Free Energy=         0.171472
 Sum of electronic and thermal Free Energies=         -274.669748

The Thermal correction to Gibbs Free Energy is calculated by:

The Sum of electronic and thermal Free Energies is the sum of the above Thermal correction and the electronic energy (also known as the single point energy since its the energy at a single point on the potential energy surface).² This thermally-corrected single point energy is the value that should be used to calculate free energies of reaction ($\Delta G_{rxn}$).

Gaussian calculates the single point energy of each intermediate geometry it generates during optimization as well as at the start of a vibrational frequency analysis. We can exploit this fact to save us from having to set up another calculation. To find the single point energy search eqMeCyhex.log for the last occurrence of SCF Done:

 SCF Done:  E(RM062X) =  -274.841184603     A.U. after    9 cycles

With this value the relationship between these three quantities becomes clear.

SCF energy: E(RM062X)                           =     -274.841184
Thermal correction to Gibbs Free Energy         =        0.171472
--------------------------------------------------------------------------
E(RM062X) + Thermal correction                  =     -274.669748
Sum of electronic and thermal Free Energies     =     -274.669748

🎉🎉 That's all folks!!! 🍾🍾
You know everything you need to run your own Gaussian jobs!

In our final lesson we’ll see how we can use Gaussian to calculate relative conformational energies.

A note on split basis calculations

It is common in large systems to use a smaller set of basis functions to find the optimized geometry (this is part of the Long Course) and then use a larger basis set to recalculate the single point energy. In this case the calculated Sum of electronic and thermal Free Energies and the thermally-corrected single point energy derived from the larger basis set will not be the same.

You must manually correct single point energies when running split-basis calculations.

References

(1) Thermochemistry in Gaussian
(2) Potential energy surface